\(\epsilon\)-greedy Monte-Carlo (MC) Control
In this section we outline methods that can result in optimal policies when the MDP is unknown and we need to learn its underlying functions / models - also known as the model free control problem. Learning in this section, follows the on-policy approach where the agent learns to act optimally by using the same policy \(\pi\) that transitions the environment (generating experiences).
Contrast this with the off-policy approach where the agent learns to act optimally by observing experiences from a different policy (called behaviour policy \(\mu\)) than the one that tries to learn (\(\pi\)).
In the model-free prediction section we have seen that it is in fact possible, with MC, to get to estimate the state value function without any MDP model dependencies. However, when we try to do do greedy policy improvement
\[\pi^\prime(s) = \arg \max_{a \in \mathcal A} (\mathcal R_s^a + \mathcal P_{ss^\prime}^a V(s^\prime))\]
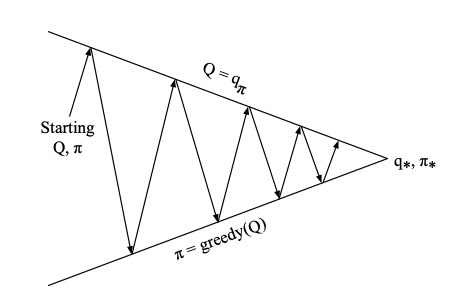
we do have dependencies on knowing the dynamics of the MDP. So the obvious question is - have we done all this discussion in vain? It turns out that we did not. All it takes is to apply prediction to the state-action value function \(Q(s,a)\) and then apply the greedy policy improvement step
\[\pi^\prime = \arg \max_{a \in \mathcal A} Q(s,a)\]
This is shown next:
Generalized policy iteration using action-value function
The only complication is that many state–action pairs may never be visited. If \(π\) is a deterministic policy, then in following \(π\) one will observe returns only for one of the actions from each state. With no returns to average, the Monte Carlo estimates of the other actions will not improve with experience. This is a serious problem because the purpose of learning action values is to help in choosing among the actions available in each state. To compare alternatives we need to estimate the value of all the actions from each state, not just the one we currently favor.
This is the general problem of maintaining exploration and we solve it by flipping a bent coin with probability \(\epsilon\) as the probability of “heads” and if we get a heads we do a greedy action while with tails (with probability \(1-\epsilon\)) we are taking a random action.
This is allowed under the general interaction afforded by the Generalized Policy Iteration (GPI) framework.
The MC pseudocode encompassing \(\epsilon\)-greedy control is shown below:
Motivated by the advantages of TD prediction we can now replace the MC with TD for the prediction step and obtain SARSA - one of the most important RL algorithms. With this replacement we can increase the frequency of policy updates (from per episode to per time step) and therefore the speed of learning.